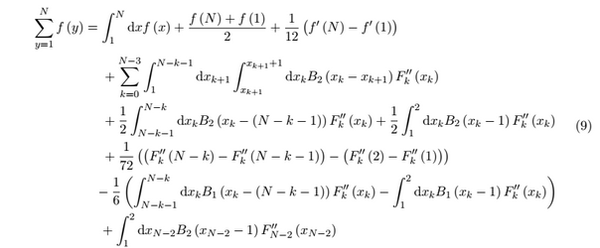Logarithmic Integral Posts
Polylogarithmic Integrals
In this topic, we use a variety of techniques to carry out logarithmic integrals from series expansions to logarithm algebra to interchanging order of integration and limit. For polylogarithms, I recommend that one carries out a special algebra of integration by parts until one polylogarithm is converted to a natural logarithm (Li1(x) = -ln(1-x)), then evaluate directly. Evidently, polylogarithms introduce more complexity than powers of natural logarithms, as one can see from the earlier posts in this logarithmic integrals section.
Click Image for Full Write-Up!
Natural Logarithm Integrals - Limits 1
For natural logarithms, I recommend a brute force method of converting the natural logarithm to a limiting expression that is far simpler, then evaluating the integral, then evaluating the limit. This interchange of order of limit and integration seems to be possible, at least for some of the early integrals that I have attempted - in fact, the method seems to produce solutions that are more compact in terms of the hypergeometric function than is found with other methods. More work is needed to test the versatility of this method - I have found some cases where the method falls short. For this method, the use of computer algebra software is certainly necessary to organize the answer.
Click Image for Full Write-Up!
Natural Logarithm Integrals - Algorithms
In this post, I introduce in full detail a method for using software to find compact solutions to integrals involving the natural logarithm. The solution in Equation 5 found to the problem in Equation 3 is posed directly to the solver. This method is computationally intensive, but in the end provides a simple result in terms of Gauss hypergeometric functions (one line, three terms only). This post is rather general, and the algorithm recommended can be applied to many problems involving integrals of powers of the natural logarithm.
Click Image for Full Write-Up!
Natural Logarithm Integrals - Series Expansion 1
In this post, I lay out a method of tackling a family of challenging logarithmic integrals via the method of expressing logarithms as a series expansion involving the Stirling Numbers of the First Kind. I found this relation (somewhat unspecified, for generalities sake) in terms of a series of the generalized Harmonic Numbers. This relation, though tedious to find the general form of the Stirling Numbers of the First Kind in terms of a series of generalized Harmonic Numbers, is useful and worth investigating in the future. For techniques for finding expressions for the Stirling Numbers of the First Kind, see the dedicated posts on this blog.
Click Image for Full Write-Up!
Unsigned Stirling Numbers (1st Kind) Posts
Analytical Expressions (Induction)
In this topic, we specify a problem where the goal is to find an analytical formula for the Stirling Numbers of the First Kind in terms of only n composed of a series of the generalized harmonic numbers of order determined by the value of k. This induction method I've found impractical for high values of k, but I have derived expressions for values of k <= 7. These expressions are particularly remarkable in the sense that the harmonic number series, Hm, is never an integer for any m > 1, but yet the linear combination of generalized harmonic numbers gives an integer for all n for a given k. This was my first post on this blog.
Click Image for Full Write-Up!
Analytical Expressions (Generating Function)
While scanning a paper looking for solutions to harmonic number sums, and I came across an astonishing paper by Zheng in 2007, which contained a finite product that I proved when expanded as a sum, generated the closed form of the Stirling Numbers of the First Kind that I derived from induction in my last post. This tool is very efficient for deriving these expressions, and my work in the post demonstrates that it is indeed the desired generator. Also found in this paper are many infinite sums involving terms comprised of the generalized Harmonic Number series.
Click Image for Full Write-Up!
Future Work (Analytical Expressions)
I am interested in examining what kinds of patterns may exist in terms of k for each analytical expression of the Stirling Numbers of the First Kind. If this area of study could be justified by considering enough particular expressions, it perhaps could give insightful ideas for predicting the coefficients of higher k expressions.
Sinc Power Integral Posts
Lobachevsky's Formula (Introduction)
I first came across the idea of Lobachevsky's formula off of social media, but I later found a recent paper (Jolany 2018) explaining the theory from first principles. This paper provides the foundational ideas for a very efficient algorithm for finding the solution to a variety of problems related to the integral of the sinc function raised to a positive integer power. This algorithm is easy to implement and customize for a variety of potential problems.
Click Image for Full Write-Up!
Sinc Power Integral (Problem Statement)
This integral problem arose from studying Lobachevsky's formula. First, in this post I differentiate between two different ways of approaching this problem - only one is interesting: we take the zeros of the sine function, then separate the integral into positive and negative contributions. We then take the absolute value of the integrand, then we take the power. The idea is to find the optimal real value of p for maximizing Ip. This problem is one that I will study for future work.
Click Image for Full Write-Up!
Riemann Hypothesis Posts
Riemann Hypothesis Introduction
This post is the initial introduction to the Riemann Hypothesis Millenium Prize problem. This problem is quite anticipated as a proof would have significant implications on our knowledge of the distribution of the prime numbers. The problem statement is as follows: are all the non-trivial zeros of the Riemann Zeta function on the critical line of Re(s) = 0.5? Over 10 billion zeros have been found to follow this rule numerically, while none have been found to negate it. Yet, mathematicians insist that until a formal proof is developed for this problem, there is no way to know if the general rule follows always. For this reason and general interest, I have decided to pursue this problem, though admittedly I have found it quite intractable. I will continue to pursue this problem as I navigate and learn more about all kinds of math - it is truly an honour to be able to comprehend such an important problem!
Click Image for Full Write-Up!
Riemann Zeta Relation to Prime Numbers
This post is about two things: 1. Showing a relation between Riemann Zeta and the prime numbers, and 2. Showing how the Riemann Zeta function is inherently more sophisticated in the analytic continuation when 0 < Re(s) < 1 than it is for Re(s) > 1. This is shown nicely in this post.
Click Image for Full Write-Up!
Riemann Hypothesis Future Work
I hope to find future inspirations to carry out interesting mathematics related to this problem. I have many documents that I have started and realized how intractable this problem is to even simple investigation - this is why the bounty is 1 million USD! I will keep looking for new ways to go farther with this investigation.
Mathematical Induction (Integration)
This is one of the first posts I ever made on this site, and it outlines a philosophical discussion of the method of induction. As a result, it finds that the analogous idea of induction in integration is differentiation. This solidifies the idea that
Click Image for Full Write-Up!
Nature of Infinity (Summation)
This post was motivated by the idea that we often specify infinite bounds on sums rather arbitrarily, when what we really mean is up to the level at which the summand vanishes. This idea is explored, for one, in the example of the generating function of the Bernoulli polynomials. A more complex example is also explored where the results are less clear cut, but where there are still very important considerations of what is meant by taking the upper bound to infinity. This post is one of my philosophy posts that provides substantial room for reflection and investigation.
Click Image for Full Write-Up!
Proof Philosophy: Stirling Generator
This post is included in philosophy rather than the section about Stirling Numbers of the First Kind since it primarily pertains to proof writing and logical reasoning. Though as an engineer I am not well practiced in proof writing, my analysis here provides some motivation for thinking creatively about what is required for rigourous proof. I encourage you to fill in the gaps I have left here - I hope you find this educational.
Click Image for Full Write-Up!
Concept Philosophy: Slowest Converging or Diverging Sum?
The topic of this post is the concept philosophy behind if there is a slowest converging or diverging series. When I first started learning about this problem, I thought that the harmonic series must be the slowest diverging series. However, after investigating, I found that there is always a way to find a slower converging or diverging series given some candidate series - as is exemplified in the image and document below. This work is very interesting for checking ones intuitions about mathematical convergence and the infinite series, as is needed to judge the applicability of theorems such as Fubini's theorem for the interchange of order of summation.
Click Image for Full Write-Up!
Introduction to Euler-Maclaurin Theory
This post gives a derivation for the Euler-Maclaurin theory to be discussed in this section. Particular interest is given to the definition of positive integer p, as it involves increasing number of derivatives of the function f. This formula is useful because it allows for a sum over the integers to be expressed as integrals over the real numbers. Particular emphasis should be paid to the alternating sign of the Bernoulli numbers and the definition of the periodic function P in terms of the Bernoulli Polynomials.
Click Image for Full Write-Up!
Power Sum by Euler-Maclaurin Formula
This post is about solving the power sum, one of the most common finite sums in mathematics. One way to solve this sum is by implementation of the Euler-Maclaurin formula, with the number of derivatives being great enough that all further derivatives go to 0, making a finite summation. The unique Euler-Maclaurin implementation expresses the answer in terms of a series of the Bernoulli numbers. This solution simplifies to the polynomial results for the sum of N positive integers raised to the positive integer power.
Click Image for Full Write-Up!
Hyperfactorials using Euler-Maclaurin
This post is about finding an asymptotic formula (analogous to Stirling's formula for the Gamma function) for the hyperfactorial H(n) using the Euler-Maclaurin formula. This post is a departure from the interests that I have expressed in many other posts, making it a unique detour towards diverse knowledge of mathematics.
Click Image for Full Write-Up!
Iterative Euler-Maclaurin Formula
This post is composed of two documents (see two images below). It outlines a formalism for iteratively applying Euler-Maclaurin to the integral sum of the remainder term for p = 2. This find a result with a far smaller remainder, but is quite a bulky expression that requires some study to implement. Nonetheless, it is interesting to study for analytic functions, as the power series decreases by 4 every iteration (see second image). The iterative Fk'' scales down by a special factor that depends on f(x) but that is always close to 0 by virtue of the ''magical'' Bernoulli Number formalism of the Euler-Maclaurin theory. This idea was an original one that I pursued in March 2025, so I felt it was worth bringing here, even if it not truly that useful.
Click Image for Full Write-Up!
Future Work: Euler-Maclaurin Formula
In the future, I have aspirations to carry out a Euler-Maclaurin formula calculation paired with a Lobachevsky formalism for the Pp functions that would satisfy the periodicity conditions for Lobachevsky application. I have yet to find a noteworthy application to carry out this idea on, but it is something I will continue thinking about in the future!
Fourier Series
Introduction to Fourier Series
This post is an introduction to Fourier Series. The focus is on the test development of the theory of the Fourier Series PDE that is the focus of the next posts in this section. This post makes clear the 2 variable formalism of the Fourier coefficient, cn. This post also lays the foundation of the emergence of a Dirac delta-like function to be discussed in future posts. The power of the orthonormal basis of complex exponentials is strongly featured, forming the foundation of Fourier Series method.
Click Image for Full Write-Up!
Fourier Series PDE - Formalized
This post verifies the effective nature of the Fourier Series PDE in the case of the analytic, Taylor-expandable function. This post builds on the verification found in the last post. This is very interesting from a perspective of verifying in a widely applicable, general way that the PDE can be trusted. This post also shows very well the potential for the method to be used in many situations with different differential and variable particular values the fundamental behaviour of the Fourier coefficient. One significant finding of this post is that the sophisticated nature of the Fourier coefficient lies with its dependence on n, not L.
Click Image for Full Write-Up!
Fourier Series Relation to Riemann Zeta Function
This post is about the development of very general analysis of the Fourier coefficient that gives rise naturally to an analytic expression for the Riemann Zeta function of even positive integer argument. This analysis was one of my first successful developments from the study the Riemann Zeta function (for more, see the Riemann Hypothesis section.
Click Image for Full Write-Up!
Fourier Emergence of Dirac Delta-like Function
In this post, I outline two things - 1. A summation solution found using Mathematica's help for the sum of complex exponentials of imaginary integer power, and 2. How that series solution directly leads to a Dirac delta-like function in an integral which provides / verifies results consistent with the Fourier formalism.
Click Image for Full Write-Up!
Fourier Independence on Interval Length L
In this post, I outline a method for finding alternative Fourier representations of a periodic function g(x). This method involves integrating the Fourier Series with respect to the interval length L, and then using the constant value of the function on the interval to find alternative representations of functions in terms of the exponential integral. This formulation was used on a test function in this post to find an interesting particular case of a series involving Pi and imaginary i that equals to exactly 1. I may do more work on this idea in future posts. Enjoy!
Click Image for Full Write-Up!
Fourier Series Using Sine and Cosine Integrals
In this post, I outline a method for representing Fourier series in terms of sine and cosine integrals. This method is further specified in terms of even and odd parts of the function g(x) being modelled by the Fourier series. This formulation is then tested using g(x) = x and g(x) = 1, and the expected solution is reproduced. We can in the future evaluate the equation by Taylor expanding g(x) to obtain a very general verification of the derived equation's correctness. This idea will be done in future work. This formulation builds strongly on the decomposition of the exponential integral of purely imaginary argument. Enjoy!
Click Image for Full Write-Up!
Fourier Future Work
There are some ideas I have for the future, such as calculating integrals using Fourier Series representations. I look forward to examining this in more detail in the future.
Repeated Integration - Incomplete Gamma Integrals
There is a hidden utility of using Cauchy's formula for a single multiple integral formula as a summation for simple test functions for which there are multiple single integrals can be easily calculated and known. This trick can be used to find integrals involving the incomplete gamma function using basic integration methods. This post is a longer post that carries out several quite tricky integrals using only basic calculation ideas. This post serves as a rudimentary beginning to thinking about fractional calculus where multiple integration formula is considered, with the same formula structure that can be abstracted to thinking about fractional integrals.
Click Image for Full Write-Up!
Fractional Calculus Introduction
This post investigates the fractional integral formula, and specifically finding the average of the fractionally integrated function from order 0 to order 1. This involved the calculation I first learned of in several places from this blog, and serves as a very interesting introduction to the idea of fractional calculus and the interpretation of the fractional derivative / integral. In the two posts attached, I do the integral with respect to the order of integration (first image), as well as the derivative with respect to the order of integration (second image). These methods are something I will explore more in future posts, including if it may be possible to carry out the integral in the first image to see the correlation between the average of the function space and the original function. In this way, this idea would be related to doing statistical analysis on the function space.
Click Image for Full Write-Up!
This post explores a relationship between fractional integration and its inverse, differentiation. This post finds an identity where the result is independent of the calculus order alpha, but incorporates in summation and integration an expression that depends on alpha in a non-trivial way. This is exciting work and something that I will continue to build on in the next post! Happy Sunday!
Click Image for Full Write-Up!
This post explores a follows up on the relationship developed in the last "Identity Fractional Calculus" post, where calculations from fractional integration and its inverse, differentiation, are used to develop relations that are independent of various free parameters. In this post, I show that for Taylor expandable functions, this relation leads trivially to the results one would suspect, bolstering the equation's credibility for producing correct results that are independent of free parameters. I then use this relation to give an equation for Pi that is independent of two free parameters (though, numerically, not all combinations of these two parameters seem to yield expected results). Finally, this equation is used to solve a relatively complicated integral in terms of a less complicated integral for which I find the solution for at the end of this post. Have an excellent weekend!
Click Image for Full Write-Up!